Il tempo assoluto non esiste perché le masse lo curvano

Il tempo assoluto tanto caro a Newton e che ci sembra tanto naturale non esiste. Le teorie della relatività, ristretta prima e generale poi, ci hanno insegnato, teoricamente prima e a suon di esperimenti poi, che il tempo corre in maniera totalmente diversa a seconda di dove mi trovo, di come mi muovo, e di cosa c’è intorno a me. Al mare scorre più lentamente che in montagna e addirittura si fermerebbe se riuscissi a raggiungere e “cavalcare” un buco nero (leggi qui e qui).

Soffermiamoci un po’ di più su questo punto: che cosa vuol dire che il tempo scorre diversamente a seconda di dove sono, di come mi muovo e di cosa succede attorno a me? Vuol dire che l’intervallo temporale tra due eventi è diverso a seconda di dove sono, di come mi muovo e di cosa succede attorno a me tra quei due stessi eventi. Se durante una gara di velocità tra lumache, noi rimaniamo a sonnecchiare a bordo pista fino alla fine, mentre tu, stufo di aspettare, ti fai un giro in macchina nei monti vicini per tornare solo allo “sprint finale”, l’intervallo temporale tra l’inizio e la fine della gara sarà diverso per noi e per te. Il nostro intervallo temporale sarà minore del tuo, ovvero per noi sarà passato meno tempo e tu sarai invecchiato di più. La lumaca sulla quale avevamo puntato tutto potrebbe aver battuto il record della pista per noi, ma non per te. L’unità di tempo, il secondo, per una persona sulla Terra non è un secondo per una persona sulla stazione spaziale internazionale. Il metro temporale, quindi, non è unico e si modifica in maniera dinamica a seconda di quanto vicino io sia ad una massa, di quanto veloce mi muova e di come masse ed energia si muovono attorno a me. Questo è la grande rivoluzione sull’idea di tempo cominciata un secolo fa.

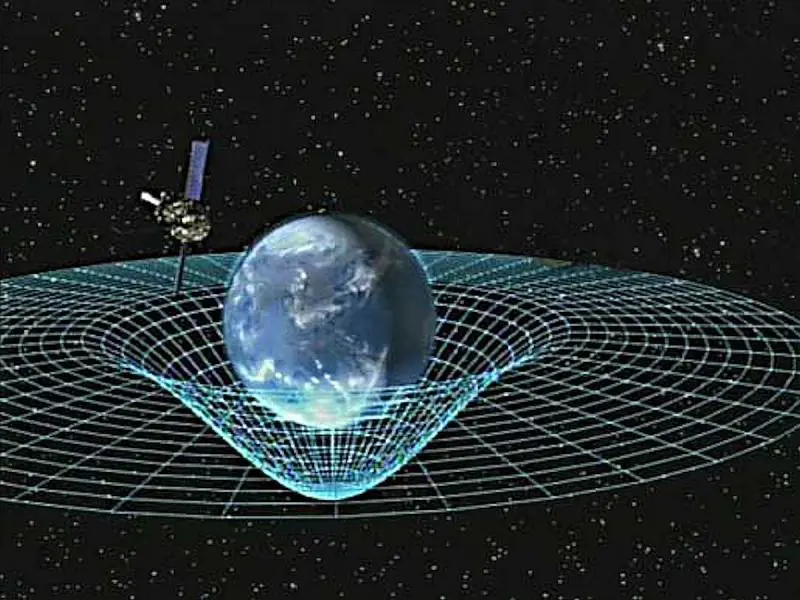
E lo spazio? Beh lo sappiamo: la relatività generale ci dice che una grande massa lo curva. È anche facile da capire e da immaginare, basta mettere un peso su di un tappeto elastico ed ecco che quest’ultimo si curva. Muovo quella massa, o ne aggiungo un’altra facendole danzare una intorno alla prima, ed ecco che la curvatura del tappeto cambia continuamente, anche producendo onde (l’equivalente delle onde gravitazionali). Le cose in realtà non sono poi così semplici. L’esempio del tappeto ha infatti i suoi grandi meriti per aiutarci a visualizzare la curvatura dello spazio, ma bisogna stare attenti: lo spazio tridimensionale infatti si curva senza andare ad occupare una quarta dimensione spaziale (che fino a prova contraria non esiste) come invece fa il tappeto bidimensionale invadendo la terza dimensione. In termini tecnici lo spazio si curva intrinsecamente e non estrinsecamente. Non entriamo in ulteriori dettagli perché proprio sulla curvatura dello spazio è interamente dedicato il nostro precedente articolo (leggi qui).

Ricapitoliamo: la relatività generale ha preso il tempo e lo spazio assoluti newtoniani che tanto ci piacciono e ci sembrano intuitivi, e li ha resi concetti fluidi, cangevoli e apparentemente controintuitivi. Sotto l’effetto di grandi masse ed energie lo spazio viene curvato (con le dovute accortezze di cui sopra), e il metro temporale perde la sua unicità, dilatandosi e restringendosi. Bene. Più o meno chiaro? Ottimo, allora riconfondiamoci le idee.

Avrete sicuramente sentito dire, infatti, che nella rivoluzione einsteiniana dell’inizio del secolo scorso spazio e tempo smettono di essere entità distinte. Essi si fondono a formare lo spaziotempo, il tessuto quadridimensionale che, modificandosi sotto la presenza di masse ed energia, produce quello che noi chiamiamo attrazione gravitazionale. Abbiamo visto infatti che il tempo si modifica a seconda di dove sono nello spazio, così come lo spazio si modifica dinamicamente nel tempo, rendendo i due totalmente interconnessi e sullo stesso piano. In relatività generale non esistono più lo spazio e il tempo, esistono stelle, asteroidi, persone ed oggetti che interagiscono con lo spaziotempo, si muovono nello spaziotempo, modificano lo spaziotempo, e vengono tirati e strattonati dallo spaziotempo.

Se quindi spazio e tempo sono così interconnessi, come è possibile che il loro modificarsi a causa della presenza di grandi masse sia così diverso?

La risposta è che modifiche nella curvatura intrinseca e modifiche del metro sono in realtà due facce della stessa medaglia. Così come spazio e tempo sono entità inscindibili, così lo sono il metro temporale e quello spaziale: assieme formano il metro spazio-temporale. Più precisamente, formano l’oggetto fisico fondamentale del quale la relatività generale descrive la dinamica, ovvero la metrica spazio-temporale che definisce le distanze (spaziali e temporali) tra due eventi. Ricordate che a scuola vi hanno insegnato che la distanza tra due punti di coordinate (x₁,y₁,z₁) e (x₂,y₂,z₂) nello spazio è √[(x₁ - x₂)² + (y₁ - y₂)² + (z₁ - z₂)²]? Questa è la distanza definita dalla comune metrica euclidea. Se cambia la metrica cambiano le distanze tra i due punti con le stesse coordinate. Se ci aggiungo la dimensione temporale, ecco che avrò ottenuto una metrica spazio-temporale in grado di definirmi distanze spazio-temporali. Il punto è che matematicamente la curvatura intrinseca è totalmente determinata dalla metrica. Se cambia la metrica cambia la curvatura, e se la curvatura cambia, allora vuol dire che è cambiata la metrica. Quello che abbiamo capito quindi è che la relatività generale dice che l'effetto della presenza e del moto di masse ed energia sullo spaziotempo è quello di cambiare dinamicamente la metrica spaziotemporale.

E questo implica che lo spaziotempo si curva, nel senso che la curvatura intrinseca del tessuto quadridimensionale cambia di conseguenza.