Così si curva lo spaziotempo

Sì, lo sappiamo: è giunto il momento di affrontare l’annosa questione dello spaziotempo che si curva. Lo abbiamo accennato in molti degli articoli passati, rimandando a tempi migliori una spiegazione più approfondita. Quei tempi migliori sono arrivati. Lo spaziotempo, dicevamo, è curvo. Il quanto e il come si curva o si appiattisce, cioè la sua curvatura, dipende dalle masse ed energia presenti, cambia in continuazione qua vicino a noi, così come là vicino a due buchi neri che ballano, e addirittura si propaga sotto forma di onde. “Si, ok, state nuovamente sorvolando, cercate di confonderci parlando di buchi neri e onde gravitazionali”, penserete. “Ma che diavolo vuol dire che lo spaziotempo è curvo?” Avete ragione. Che lo spazio si curvi si può anche capire. Ma il tempo?

Andiamo allora con ordine e per ora dimentichiamoci del tempo per concentrarci solo sullo spazio. Che in realtà, come vedremo, non è così semplice da capire come uno potrebbe immaginare.

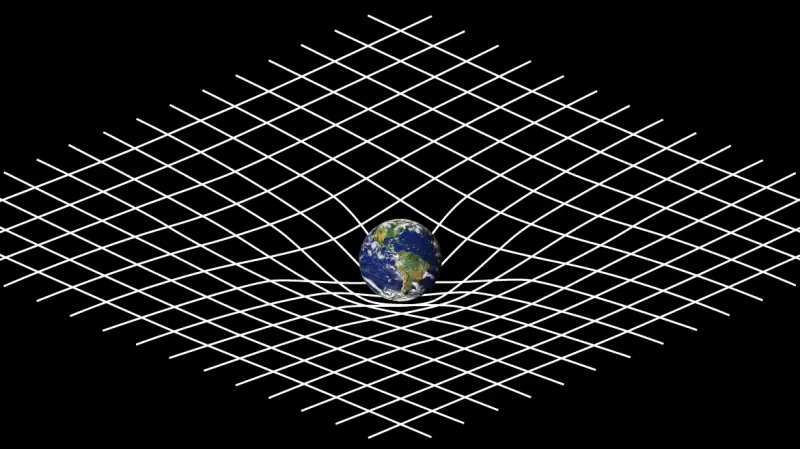
Uno spazio curvo possiamo immaginarlo e sappiamo cos’è (oltre al titolo di questa rubrica): la superficie di un pallone da basket, per esempio, è curva (in particolare è sferica). E sappiamo anche visualizzare come una massa possa curvare lo spazio sfruttando il classico esempio del telo elastico: se sopra un bel telo elastico piatto appoggio un pallone, il primo si deforma curvandosi sotto il peso della palla a spicchi. Più grande è la massa, maggiore sarà la deformazione.

Ora prendiamo una piccola pallina di polistirolo. Se la lanciassimo sopra un telo piatto, questa correrebbe dritta senza esitazioni. Ma se la lanciamo sul telo “deformato” di cui sopra, allora seguirà una rotta diversa, orbitando magari intorno al pallone da basket per poi andarci a sbattere contro. È in questo modo che si spiega l’attrazione gravitazionale attraverso la curvatura dello spazio: due masse (la palla da basket e la pallina) non si attraggono tra loro perché tirate da una forza che agisce nello spazio, come diceva Newton, ma “cadono” l’una sull’altra scivolando sul tappeto deformato dalle loro stesse masse. Per usare le 12 parole con cui John Wheeler riassumeva la relatività generale di Einstein: Space-time tells matter how to move, matter tells space-time how to curve, ovvero “lo spaziotempo dice alla materia come muoversi, la materia dice allo spaziotempo come curvarsi”.

Benissimo, non sembra nemmeno così difficile. Se ci pensiamo un po’ meglio, però, il telo dell’esempio, che è bidimensionale, si deforma andando ad occupare la terza dimensione disponibile. Nell'Universo però non funziona esattamente così. Secondo la relatività generale, infatti, massa ed energia curvano lo spazio tridimensionale nella sua interezza. Curvano cioè tutto l’Universo. E allora in cosa lo curvano? In cosa lo deformano? Cosa può andare ad occupare lo spazio se non è immerso in nient’altro?

Per spiegarlo, torniamo a pensare al pallone da basket che, come detto, è curvo. Poniamoci questa domanda: come facciamo a sapere che la palla è curva? La risposta più semplice sarebbe: "Beh, si vede, no?". Ma ora immaginiamo, un po’ come in Flatlandia di Edwin Abbott Abbott (se non lo avete fatto, leggetelo, è geniale!), che la superficie del pallone sia abitata da esseri pensanti, bidimensionali anch’essi, i quali non siano consapevoli dell’esistenza di una terza dimensione. Per questa popolazione, che chiameremo gli Smilzi, l’intero universo è la superficie bidimensionale del pallone e non esiste altro, essendo essi inglobati nella superficie stessa, senza un “sopra” né un “sotto”. Secondo voi, ArchiSmilzo, il più intelligente tra la popolazione della palla a spicchi, può sapere se l’universo in cui vive è curvo oppure no? Per lui quel “Beh, si vede” non è più una spiegazione valida: ArchiSmilzo infatti non vede il pallone “da fuori” immerso nel mondo tridimensionale come noi. Anche riuscissimo a comunicare con lui e provassimo a spiegargli che noi vediamo una sfera, difficilmente riusciremmo a convincerlo.

Il nostro geniale amico, però, scopre che se lascia il suo cane bidimensionale passeggiare sempre dritto senza mai fermarsi, ad un certo punto lo vedrà tornare al punto di partenza, spuntando alle sue spalle. ArchiSmilzo, che ha seguito attentamente le lezioni del grande SmilzEuclide, ricorda che in un mondo piatto questo non è possibile, e deduce quindi che lo spazio in cui lui vive in realtà è curvo. Non lo “vede” da fuori, ma lo deduce. In termini matematici, questa è la differenza tra i concetti di curvatura estrinseca e curvatura intrinseca. La curvatura estrinseca di una superficie è quella che “si vede” se guardiamo la superficie stessa immersa in uno spazio che possiede una dimensione in più. (Ad esempio: la superficie della sfera, che come detto è bidimensionale, noi umani possiamo vederla perché è immersa nel nostro mondo tridimensionale). La curvatura intrinseca, invece, è, come dice il nome stesso, una proprietà unicamente della superficie, indipendentemente dal fatto che sia immersa o meno in uno spazio esterno. La si deduce osservando le stranezze che possono accadere su di una superficie curva: cani che tornano indietro, linee parallele che si incontrano, ed altre ancora. E la si definisce e quantifica precisamente grazie a concetti e strumenti matematici molto più sofisticati di lasciare il proprio cane camminare sempre dritto.

Attenzione: la sfera è curva sia intrensicamente che estrensicamente, ma i due concetti sono totalmente indipendenti. In particolare, si può pensare una superficie con curvatura instrinseca che non sia immersa in nessuno spazio, e che per la quale non ha proprio senso definire la curvatura estrinseca.

Quella che sembra un'ulteriore complicazione, è in realtà la soluzione alle domande che ci eravamo posti qualche riga fa riguardo alla relatività generale. Avevamo detto infatti che una massa curva lo spazio nella sua interezza. E ci chiedevamo in “cosa” lo deforma visto che non è immerso in nient’altro. La soluzione quindi è che la presenza di massa ed energia cambia la curvatura intrinseca dello spazio che la circonda senza necessariamente andare ad invadere una quarta dimensione spaziale. La storia della masse che non si attraggono tirate da una forza, ma scivolano nello spazio curvo, con le dovute accortezze, rimane dunque valido.

È solo maledettamente più difficile da visualizzare e digerire perché è difficile visualizzare la curvatura intrinseca di una superficie. Noi esseri umani tridimensionali siamo gli Smilzi nel nostro Universo tridimensionale. Con la differenza che una quarta dimensione spaziale proprio non esiste… Fino a prova contraria.